Tavallinen monikulmio

Polyhedron sanotaan olevan säännöllinen , jos se koostuu täysin identtisiä ja säännöllinen kasvot , ja jos kaikki sen kärjet ovat identtisiä (jos on sama määrä reunoja, jotka lähenevät toisiaan jokaista pistettä).

On olemassa viisi säännöllistä kuperaa polyhedraa , jotka tunnetaan nimellä platoniset kiinteät aineet .

On olemassa neljä säännöllistä kuperaa polyhedraa, jotka tunnetaan nimellä Kepler-Poinsot kiinteät aineet .

Platoniset kiinteät aineet

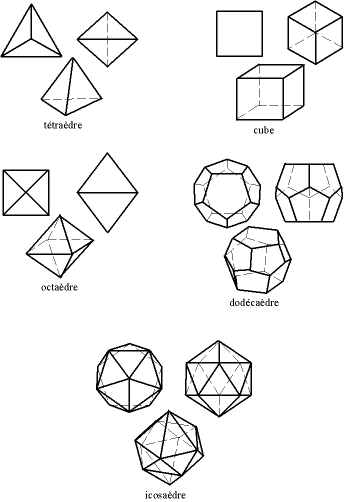
Näyttää siltä, että Pythagoras itse (noin 530 eaa. ) Tai Pythagorean Taranton arkkilainen (noin 360 eKr. ) Löysi kolme ensimmäistä viidestä: tetraedri (pyramidi), heksahedroni (kuutio), dodekaedri. Sitten Ateenan Theaetetus (kuoli 395 tai 369 eKr. ) Löysi kaksi muuta: oktaedrin ja ikosaedrin. Platon käyttää niitä syvälle Timaeuksessa (54c - 56c), joka on peräisin vuodelta 358 eKr. AD Euclid tutkii ne hänen Elements (n. 300 eaa)

Tavallinen tetraedri (pyramidi)

Säännöllinen tetraedri ( tetra , neljä ja èdre , pohja), polyhedron, jossa on 4 kolmiota,

koostuu 4 kasvosta tasasivuisessa kolmiossa,
on 4 kärkeä ja 6 reunaa.

Tavallinen heksahedroni (kuutio)

Heksahedroni ( heksa , kuusi ja èdre , pohja)

koostuu 6 neliöpinnasta,
siinä on 8 kärkeä ja 12 reunaa,
on 24 tasakylkistä suorakulmaista .

Tavallinen oktaedri

Oktaedrin (vuodesta okta kahdeksan, ja èdre , base)

koostuu kahdeksasta kasvosta tasasivuisessa kolmiossa,
on 6 kärkeä ja 12 reunaa,
on 48 suorakulmaista skaalaa.

Tavallinen dodekaedri

Dodekaedri ( dodekasta , kaksitoista, ja edron , pohja)

koostuu 12 yhtäläisestä viisikulmaisesta kasvosta,
siinä on 20 kärkeä ja 30 reunaa.

Ikosaedri

Ikosaedri ( ikosasta , kaksikymmentä, ja èdre , pohja)

koostuu 20 kasvosta tasasivuisessa kolmiossa ,
siinä on 12 kärkeä ja 30 reunaa,
siinä on 120 suorakulmaista skaalaa.

Platonisen kiinteän aineen pintojen keskukset ovat platonisen kiinteän aineen kärjet. Tämä kirjeenvaihto on sisäinen tetraedrien keskuudessa; se vaihtaa kuutioita ja oktaedroja toisaalta, dodekahedraa ja ikosaedraa toisaalta.

Platon piti näitä kiinteitä aineita täydellisyyden kuvana; hänelle, kuten hän selittää Timaeuksessa , tetraedri on tulen symboli, oktaedri ilmaa, ikosaedri veden, kuutio maan ja dodekaederi koko maailmankaikkeuden.

Kaksi Cauchyn julkaisua Journal de l ' École -polytekniikassa käsittelee tavallisia polyhedraa.

Klassinen matematiikka koskee näiden viiden säännöllisesti kiintoaineet käsitteestä ryhmä .

Esittely

Osoitamme, että Platonissa voi olla vain viisi säännöllistä kuperaa polyhedraa; tämä mielenosoitus vastaa Euclidia.

käyttöehdot

Olkoon $m$ kasvojen reunojen lukumäärä, $n$ monikulmion kärkipisteessä kohtaavien kasvojen lukumäärä ({ m , n } on monikulmion Schläfli-symboli ). Tiedämme sen :

$m$ ja $n$ ovat luonnollisia lukuja;
$m \geq 3$ , koska monikulmiossa, joka on kaksiulotteinen kuvio, on vähintään kolme reunaa;
$n \geq 3$ , koska kolmiulotteisen kärjen piste, joka on kolmiulotteinen, ei voi liittää alle kolmea pintaa;
säännöllisen $m-$ polygonin kulma on yhtä suuri kuin asteet: 60 astetta tasasivuisella kolmiolla, 90 neliöllä, 108 tavallisella viisikulmalla, 120 tavallisella kuusikulmalla jne. ; ${\ displaystyle {\ frac {180 (m-2)} {m}}}$
kärjen kulmien summa $s$ on ehdottomasti alle 360 astetta, muuten pinnat ovat samansuuntaisia ( $s$ = 360 astetta) tai päällekkäisiä ( $s$ > 360 astetta).

Yhtälö

Siksi on kyse seuraavan järjestelmän kaikkien ratkaisujen löytämisestä:

{\ alkaa {tapaukset} m, n \ muodossa {\ mathbb N} \\ m, n \ geq 3 \\ s (m, n) = {\ frac {180n (m-2)} {m}} <360 \ loppu {tapaukset}}

Ratkaisut

Jos m = 3 (kolmiopinnat), sopivat arvot ovat:
- $n = 3$ , koska $s (3,3) = 180 <360$ : se on tetraedri
- $n = 4$ , koska $s (3,4) = 240 <360$ : se on oktaedri
- $n = 5$ , koska $s (3,5) = 300 <360$ : se on ikosaedri
- Jos $n \geq 6$ , tulos on liian suuri: $s (3,6) = 360$ . Itse asiassa on kuusi tasasivuista kolmiota, joilla on yhteinen kärki, muodostaen siten säännöllisen tasaisen kuusikulmion.

Jos m = 4 (neliönmuotoiset pinnat), ainoa ratkaisu on:
- $n = 3$ , koska $s (4,3) = 270 <360$ : se on kuutio
- Jos $n \geq 4$ , tulos on liian suuri: $s (4,4) = 360$ . On todellakin neljä neliötä, joilla on yhteinen kärki, muodostaen siten tasaisen neliön.

Jos m = 5 (viisikulmaiset kasvot):
- $n = 3$ , koska $s (5,3) = 324 <360$ : se on dodekaederi.
- Jos $n \geq 4$ , tulos on liian suuri: $s (5,4) = 432> 360$ .

Jos $m \geq 6$ , ei ole enää liuos: $s (6,3) = 360$ , ja jos $m \geq 6$ sitten $s ( m , n ) => 360$ kaikilla $n \geq 3$ .

Kaksinaisuus

Tämä menetelmä mahdollistaa myös kaksoispolyhedran tunnistamisen , koska $m$ ja $n$ kääntäminen riittää polyhedronin kaksoisarvon saamiseksi:

tetraedrin {3,3} kaksoisvirta on itse tetraedri {3,3};
oktaedrin duaali {3,4} on kuutio {4.3};
ikosaedrin kaksoiskappale {3,5} on dodekahedroni {5,3}.

Näemme myös, että tetraedri on ainoa autoduaali, koska kun asetettu $m = n$ , yhtälön ainoa koko ratkaisu

s (n, n) = {\ frac {180n (n-2)} {n}} = 180 (n-2) <360

on $n = 3$ , koska $s (3,3) = 180 <360$ ; kun $n = 4$ , tulos on liian suuri: $s (4,4) = 360$ .

Kepler-Poinsot-polyhedra

Viiden platonisen kiinteän aineen lisäksi voimme rakentaa neljä muuta säännöllistä kiinteää ainetta, kaksi, joiden kasvot ovat säännöllisiä tähdellä merkittyjä (tai ristittyjä) polygoneja : Keplerin kiinteät aineet ja kahdella säännölliset pinnat, mutta jotka voivat tunkeutua tunkeutumaan: Poinsotin kiinteät aineet .

Pieni tähti dodekaedri löysi Kepler kaksikymmentäkaksi vuosisataa jälkeen Platon, vuonna 1619 . Siinä on 12 kasvoa, jotka ovat tähtiviisikulmioita, 12 kärkeä ja 30 reunaa. Jokaisessa kärjessä kohtaavat viisi kasvoa. Tämä pieni tähti dodekaedri voidaan nähdään mosaiikki , jonka Paolo Uccello , vuonna Pyhän Markuksen vuonna Venetsian valmistettu noin vuonna 1430 (lähes 200 vuotta ennen sen matemaattinen kuvaus).
Suuri tähti Dodekaedri , löysi Kepler, joka on muodostettu saman 12 tähti pentagons, joka on 20 pistettä ja myös 30 reunat.
Suuri dodekaedri löysi Poinsot vuonna 1809 . Sen 12 pintaa ovat säännöllisiä viisikulmioita, siinä on 12 kärkeä ja 30 reunaa. Yli 200 vuotta aiemmin Wenzel Jamnitzer kuvasi vuonna 1568 julkaistussa puupiirroksessaan Perspectiva corporum regularium -kirjassa suurta dodekahedronia .
Suuri ikosaedri , löysi Poinsot, joka on muodostettu 20 tasasivuiset kolmiot, ja joka on 12 pistettä ja myös 30 reunat.

pieni tähtikuvioinen dodekaedri {5/2, 5}
suuri tähtikuvioinen dodekaedri {5/2, 3}
iso dodekaedri
{3, 5/2}
iso ikosaedri
{5, 5/2}

Huomautuksia ja viitteitä

Lue verkossa osoitteessa Gallica .
(De) Bilder von Wentzel Jamnitzer aus der Perspectiva Corporum Regularium

Katso myös

Aiheeseen liittyvät artikkelit

Geodeettiset kupolit tai geodit
Säännölliset polykorit ovat säännöllisen polyhedran 4-ulotteisia analogeja.

Ulkoinen linkki

" Polyhedra liikkeessä " ( Arkisto • Wikiwix • Archive.is • Google • Mitä tehdä? ) , On icosaweb.ac-reunion.fr