Induktiivinen raja

Vuonna matematiikan , ja erityisesti luokkaan teoriassa ja universaali algebran , käsite induktiivista rajaa yleistää rakenteiden klassisen käsite raja johtuvat analyysiin .

Esipuhe

Induktiivinen raja on kolimiitin erityistapaus kategoriateoriassa . Samoin kuin sen kaksoisprojektiivinen raja , se on käsitteellisesti hyvin lähellä analyysissä havaittua raja-käsitettä ja osuu siihen tietyissä tapauksissa.

Ensimmäinen avainkohde on käsite rajan ylittämisestä. Positiivisten reaalilukujen raja on positiivinen. Neliöjuuren raja on yhtä suuri kuin rajan neliöjuuri. Vastaavasti , algebrassa selvitetään, mitkä ovat ominaisuudet, jotka ylittävät rajan (induktiiviset, projektiiviset tai muut). Nämä ominaisuudet eivät ole funktioita kuten analyysissä, vaan funktoreita . Induktiivisen rajan kanssa yhteensopiva kovariaattinen funktori varmistaa siten, että kuvien induktiivinen raja on yhtä suuri kuin induktiivisen rajan kuva. (Jos funktori on epämääräinen, se muuttaa induktiivisen rajan projektiiviseksi rajaksi.)

Esimerkiksi kommutatiivisen renkaan A moduulien luokassa induktiivinen raja on edelleen olemassa ja se on yhteensopiva ytimen , kuvan ja koksi . Toisaalta projektioraja on yhteensopiva ytimen kanssa, mutta ei kuvan kanssa.

Jotkut rakenteet rakennetaan luonnollisesti ylittämällä raja. Varten ääretön algebrallinen laajennus , Galois ryhmä voidaan määritellä projektiivista raja. Saamme siis profiniittiryhmän .

Toinen keskeinen kohta on tiheyden käsite. Mikä tahansa todellinen luku on rajoitettu rationaalilukuihin ja jopa desimaaleihin (mikä on perustana numeroiden käsittelylle laskimilla). Mikä tahansa segmentille määritelty jatkuva toiminto on polynomifunktioiden ja jopa porrastettujen toimintojen yhtenäinen raja . Tämä tulos antaa esimerkiksi häikäisevän esityksen Riemann-Lebesgue-lauseesta . Todistetaan ensin portaikkotoimintojen tulos ja sitten siirrytään rajaan. Juuri tämän mielentilan pyrimme toistamaan algebrassa induktiivisten rajojen ansiosta . Tuloksen suoran osoittamisen sijaan aloitamme osoittamalla sen yksinkertaisilla esineillä, sitten menemme induktiiviseen rajaan. Voimme esimerkiksi huomata, että mikä tahansa vektoritila on rajallisten ulottuvuuksien vektoritilojen induktiivinen raja.

Historiallinen huomautus

Induktiivisen rajan käsitteen otti Lev Pontriaguine käyttöön vuonna 1931 määrittämään osamäärien isomorfismin niiden vääntöalaryhmän homologiaryhmien ja (Betti-ryhmät, joilla on arvot  ; Betti-ryhmällä on vastaavan Betti-luvun sijoitus, nimittäin sen sijoitus ), jossa X on mikä tahansa kompakti osajoukko . Ryhmät , joissa pienenevä sekvenssi kompakteista yksinkertaisista leikkauskomplekseista on yhtä suuri kuin X , muodostavat suoran abeliryhmien järjestelmän, joista on "rajaryhmä" ("Limesgruppe") (toisin sanoen induktiivinen raja). Pontriagin määritteli melko yleisesti, ja kuten me tänään teemme, suoran ryhmäjärjestelmän (ei välttämättä abelialaisten) induktiivinen raja. Odotettu tulos on, että sovellukset Hs(X;Z/mZ){\ displaystyle H_ {p} (X; \ mathbb {Z} / m \ mathbb {Z})}Hei-s-1(Rei-X;Z/mZ){\ displaystyle H_ {np-1} (\ mathbb {R} ^ {n} -X; \ mathbb {Z} / m \ mathbb {Z})}Z/mZ{\ displaystyle \ mathbb {Z} / m \ mathbb {Z}}m=0{\ displaystyle m = 0}Rei{\ displaystyle \ mathbb {R} ^ {n}}Hei-s-1(Rei-EI(Tj);Z/mZ){\ displaystyle H_ {np-1} (\ mathbb {R} ^ {n} -N (T_ {j}); \ mathbb {Z} / m \ mathbb {Z})}(EI(Tj)){\ displaystyle (N (T_ {j}))}}Hei-s-1(Rei-X;Z/mZ){\ displaystyle H_ {np-1} (\ mathbb {R} ^ {n} -X; \ mathbb {Z} / m \ mathbb {Z})}

Hs(EI(Tj+1);Z/mZ)→Hs(EI(Tj);Z/mZ){\ displaystyle H_ {p} (N (T_ {j + 1}); \ mathbb {Z} / m \ mathbb {Z}) \ oikeanpuoleinen nuoli H_ {p} (N (T_ {j}); \ mathbb {Z } / m \ mathbb {Z})}, Hei-s-1(Rei-EI(Tj);Z/mZ)→Hei-s-1(Rei-EI(Tj+1);Z/mZ){\ displaystyle H_ {np-1} (\ mathbb {R} ^ {n} -N (T_ {j}); \ mathbb {Z} / m \ mathbb {Z}) \ oikeanpuoleinen H_ {np-1} ( R ^ {n} -N (T_ {j + 1}); \ mathbb {Z} / m \ mathbb {Z})}

siirretään toisistaan. Sekvenssi muodostaa käänteisen järjestelmän, jonka (projektiivinen) raja on  ; Siitä huolimatta Pontriagin jätti huomiotta projektiivisen rajan, jonka Eduard Čech näki seuraavana vuonna (1932) Pontriaginin työstä riippumatta; mutta topologisten tilojen käänteisjärjestelmän projisointirajan tarkka määritelmä annettiin vasta vuonna 1936 Norman Steenrodin toimesta . Ryhmien tai topologisten ryhmien tai topologisten tilojen projektiivisten (tai induktiivisten) rajojen muotoilu. funktoreina suorien (tai käänteisten) järjestelmien luokan ja ryhmien tai topologisten ryhmien tai topologisten tilojen jne. konkreettisen luokan välillä toteuttivat Samuel Eilenberg ja Saunders Mac Lane vuonna 1945  ; nämä käsitteet ja niiden suhteet muotoiltiin täysin yleisellä tavalla, ja Daniel Kan (en) tutki niitä yksityiskohtaisesti vuonna 1958. Hs(EI(Tj);Z/mZ){\ displaystyle H_ {p} (N (T_ {j}); \ mathbb {Z} / m \ mathbb {Z})}Hs(X;Z/mZ){\ displaystyle H_ {p} (X; \ mathbb {Z} / m \ mathbb {Z})} 

Tilattu suodatinsarja

Antaa olla järjestetty sarja (osittain tilattu yleensä). Sanomme, että se on suodatettu järjestetty joukko if (Minä,≤){\ displaystyle (I, \ leq)}(Minä,≤){\ displaystyle (I, \ leq)}

∀(i,j)∈Minä2,∃k∈Minä,i≤k et j≤k.{\ displaystyle \ forall (i, j) \ in I ^ {2}, \ olemassa k \ in I, i \ leq k \ ja \ j \ leq k.}

Sanomme, että joukko suodatetaan vasemmalla, kun suodatetaan päinvastainen järjestys . Tällöin sanavarasto säilytetään, mutta se vastaa päinvastaista järjestystä. Käytännössä tämä ei aiheuta sekaannusta, se on jopa melko käytännöllistä. Suodatusjoukko I on luokka, jonka objektit ovat I: n elementtejä ja morfismit ovat parit (lähteen i ja tavoitteen j ). (j,i),i≤j{\ displaystyle (j, i), i \ leq j}

Induktiivinen järjestelmä

Antaa olla järjestetty suodatinsarja. Antaa olla luokka. Kutsumme induktiivinen järjestelmä kohteiden indeksoitu I functor (covariant) ja I on , data perheen esineiden ja morphisms kunkin parin indeksejä siten, että koko tyydyttää: (Minä,≤){\ displaystyle (I, \ leq)}VS{\ displaystyle {\ mathcal {C}}}D.{\ displaystyle {\ mathfrak {D}}}VS{\ displaystyle {\ mathcal {C}}}VS{\ displaystyle {\ mathcal {C}}}(Ei)i∈Minä{\ displaystyle (E_ {i}) _ {i \ I}}VS{\ displaystyle {\ mathcal {C}}}fij:Ei→Ej{\ displaystyle f_ {i} ^ {j}: E_ {i} \ - E_ {j}}(i,j)∈Minä2{\ displaystyle (i, j) \ ryhmässä I ^ {2}}i≤j{\ displaystyle i \ leq j}

• ∀i∈Minä,fii=MinädEi{\ displaystyle \ forall i \ in I, f_ {i} ^ {i} = Id_ {E_ {i}}} ;
• ∀(i,j,k)∈Minä3, i≤j≤k⇒fjk∘fij=fik{\ displaystyle \ forall (i, j, k) \ in I ^ {3}, \ i \ leq j \ leq k \ Rightarrow f_ {j} ^ {k} \ circ f_ {i} ^ {j} = f_ {i} ^ {k}}.

Tämän toiminnon määrittelevät ja . D.(i)=Ei{\ displaystyle {\ mathfrak {D}} (i) = E_ {i}}D.((i,j))=fij{\ displaystyle {\ mathfrak {D}} ((i, j)) = f_ {i} ^ {j}}

Induktiivisen rajan universaali ominaisuus

Olkoon ( X i , f ij ) induktiivinen järjestelmä luokassa . Induktiivinen raja X , kun se on olemassa, on tavoitteena olevia varustettu nuolilla on X i kanssa arvot X tarkistaa, ovatko suhteet kaikille . Lisäksi tietojen on oltava yleismaailmallisia: Kaikille muille esineille Y, jotka on varustettu nuoliperheellä ψ i, jotka tarkistavat samanlaiset yhteensopivuudet, on olemassa yksi nuoli u  : X → Y , kuten kaavio: VS{\ displaystyle {\ mathcal {C}}} VS{\ displaystyle {\ mathcal {C}}}ϕi{\ displaystyle \ phi _ {i}}ϕi=ϕj∘fij{\ displaystyle \ phi _ {i} = \ phi _ {j} \ circ f_ {ij}}i≤j{\ displaystyle i \ leq j}(X,ϕi){\ displaystyle (X, \ phi _ {i})}

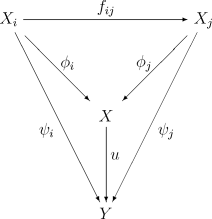
anna olla kommutatiivinen kaikille i ≤ j . Induktiivinen raja on huomattava: . Puhumme X i: n induktiivisesta rajasta siirtymämorfismien f ij mukaan tai kielen väärinkäytöllä I: n mukaisen rajan , katso yksinkertaisesti X i: n induktiivisesta rajasta . X=lim→⁡Xi{\ displaystyle X = \ varinjlim X_ {i}}

Kuten minkä tahansa universaalin ominaisuuden kohdalla , induktiivinen raja on olemassa, kun se on olemassa, yksittäiseen isomorfismiin saakka.

Toisin sanoen induktiivinen raja edustaa funktoria, joka yhdistää joukon luokan Y objektiin . VS{\ displaystyle {\ mathcal {C}}}lim←⁡Hom(Xi,Y){\ displaystyle \ varprojlim Hom (X_ {i}, Y)}

Induktiivisen rajan rakentaminen

Induktiivinen raja on olemassa useimmissa tavallista luokkiin (erityisesti magmat , monoids , ryhmät , Abelin ryhmien , renkaat , -modules , K -vektorisysteemi tilat , topologinen tiloja , jne.). Voimme rakentaa sen taustaryhmien perheen induktiivisesta rajasta. Siksi se kulkee unohtavan funktorin kanssa.

Yleisemmin sanottuna missä tahansa luokassa sen rakenne on kaksinkertainen ennusteen rajaan nähden . Rakennamme projektiivisen rajan kahdella prosessilla, tuotteen ja ytimen prosessilla . Rakennamme induktiivisen rajan kahdesta kaksoiskäsitteestä summa ja koksi .

Induktiivinen asetettu raja

Olkoon ( E i , f ij ) induktiivinen joukkojärjestelmä. Saadaan induktiivista rajaa kuin osamäärä joukko on disjoint liiton mukaan ekvivalenssirelaatio  : ⊔i∈MinäEi{\ displaystyle \ sqcup _ {i \ in I} E_ {i}}

(i,x)∼(j,y)⇔∃k∈Minä,i≤k, j≤k et fik(x)=fjk(y){\ displaystyle (i, x) \ sim (j, y) \ Leftightarrow \ olemassa k \ in I, i \ leq k, \ j \ leq k \ ja \ f_ {i} ^ {k} (x) = f_ {j} ^ {k} (y)}

Merkitään osamääräjoukko. Määrittelemiseksi otamme luokan . E∞{\ displaystyle E _ {\ infty}}ϕi:Ei→E∞{\ displaystyle \ phi _ {i}: E_ {i} \ - E _ {\ infty}}ϕi(x){\ displaystyle \ phi _ {i} (x)}(i,x){\ displaystyle (i, x)}

Olkoon ( E i , f ij ) topologisten tilojen induktiivinen järjestelmä . Aikaisemmassa rakennelmassa annamme peräkkäin alla olevien joukkojen epäyhtenäisen liiton lopullisella topologialla , sitten osamääräjärjestelmällä osamäärä topologialla (tai suoremmalla tavalla: annamme induktiivisen joukon rajan lopullisella topologialla).

Magmojen induktiivinen raja

Olkoon ( E i , f ij ) induktiivinen magmajärjestelmä. Jokaisella sarjalla on sisäinen kokoonpanolaki ja jokainen kartta on morfismi. Aloitetaan rakentamalla joukkojen induktiivinen raja . Sitten magmalla on ainutlaatuinen rakenne siten, että kanoniset kartat ovat morfismeja. Ei{\ displaystyle E_ {i}}∗i{\ displaystyle * _ {i}}fij{\ displaystyle f_ {i} ^ {j}}Ei{\ displaystyle E_ {i}}E∞{\ displaystyle E _ {\ infty}}ϕi{\ displaystyle \ phi _ {i}}

Rakennamme tämän lain seuraavasti. Let ja kaksi edustajaa kahdesta osasta . On kuten ja . Sisällä meillä on ja . Sitten asetamme , saatu tulos ei tietenkään riipu valinnasta . (i,x){\ displaystyle (i, x)}(j,y){\ displaystyle (j, y)}E∞{\ displaystyle E _ {\ infty}}k∈Minä{\ displaystyle k \ in I}i≤k{\ displaystyle i \ leq k}j≤k{\ displaystyle j \ leq k}E∞{\ displaystyle E _ {\ infty}}(i,x)=(k,fik(x)){\ displaystyle (i, x) = (k, f_ {i} ^ {k} (x))}(j,y)=(k,fjk(y)){\ displaystyle (j, y) = (k, f_ {j} ^ {k} (y))}(i,x)∗(j,y)=(k,fik(x)∗kfjk(y)){\ displaystyle (i, x) * (j, y) = (k, f_ {i} ^ {k} (x) * _ {k} f_ {j} ^ {k} (y))}k{\ displaystyle k}

Ominaisuudet

• Jos jokainen laki on kommutatiivinen , niin laki * on kommutatiivinen.∗i{\ displaystyle * _ {i}}
• Jos jokainen laki on assosiatiivinen , niin laki * on assosiatiivinen.∗i{\ displaystyle * _ {i}}
• Jos jokaisella lailla on neutraali elementti ja jos jokainen morfismi tyydyttää , niin *: lla on neutraali e (lisäksi jokaiselle i : lle meillä on ).∗i{\ displaystyle * _ {i}} ei{\ displaystyle e_ {i}}fij{\ displaystyle f_ {i} ^ {j}}fij(ei)=ej{\ displaystyle f_ {i} ^ {j} (e_ {i}) = e_ {j}}ϕi(ei)=e{\ displaystyle \ phi _ {i} (e_ {i}) = e}
• Jos kukin on ryhmä rakenne , on ryhmä.Ei{\ displaystyle E_ {i}}E∞{\ displaystyle E _ {\ infty}}

Induktiivinen rengasraja

Vastaavasti, jos jokaisella joukolla on kaksi lakia ja induktiivisella rajalla on kaksi lakia ja . Jos jokainen laki on jakautuva suhteessa , niin jakava on suhteessa . Ei{\ displaystyle E_ {i}}+i{\ displaystyle + _ {i}}∗i{\ displaystyle * _ {i}}E∞{\ displaystyle E _ {\ infty}}+{\ displaystyle +}∗{\ displaystyle *}∗i{\ displaystyle * _ {i}}+i{\ displaystyle + _ {i}}∗{\ displaystyle *}+{\ displaystyle +}

Tämä prosessi mahdollistaa siten induktiivisen rengasrajan rakentamisen.

• Jos jokainen rengas on ehjä, niin on .Ei{\ displaystyle E_ {i}}E∞{\ displaystyle E _ {\ infty}}
• Jos jokainen rengas on runko, niin on .Ei{\ displaystyle E_ {i}}E∞{\ displaystyle E _ {\ infty}}

Moduulien induktiivinen raja

Olkoon BE kommutatiivinen rengas ja ( E i , f ij ) induktiivisen järjestelmä -modules . Voimme varata taustalla olevien joukkojen induktiivisen rajan A- moduulirakenteella siten, että kartat ovat lineaarisia. Tällainen rakenne on ainutlaatuinen ja se on rakennettu samalla tavalla kuin magmille. E∞{\ displaystyle E _ {\ infty}}ϕi{\ displaystyle \ phi _ {i}}

Esimerkkejä

• Jos suodatinkokoonpanossa I on suurempi elementti (esimerkiksi jos olen rajallinen eikä ole tyhjä), minkä tahansa induktiivisen järjestelmän induktiivinen raja on yhtä suuri kuin .ω{\ displaystyle \ omega}(Ei,fij){\ displaystyle (E_ {i}, f_ {i} ^ {j})}Eω{\ displaystyle E _ {\ omega}}
• Induktiivinen raja järjestelmän indeksoitu tyhjä joukko on alkuperäisen olion .
• Olkoon E joukko ja kasvava E : n osajoukko , kanonisten injektioiden kanssa. Sekvenssin induktiivinen raja identifioidaan näiden joukkojen yhdistämisen kanssa.(Eei){\ displaystyle (E_ {n})}(Eei){\ displaystyle (E_ {n})}
• Olkoon p olla alkuluku . Kaikkien n avulla U n on syklinen ryhmä, p n : nnen juuret yhtenäisyyden käytettäessä algebrallisesti suljettu kunta. Pidämme sulkeumia siirtymämorfismina. Tämän järjestelmän suora raja on sitten ääretön ryhmä, joka muodostuu kaikista ykseyden p- ensisijaisista juurista (katso Prüferin ryhmä ).
• Olkoon E olla topologinen tilaa ja on pisteen E, siemen toimintoja ja E on on induktiivinen raja sarjaa sarjaa jatkuvaa kuvaukset tahansa -osassa U of . Naapurustot järjestetään sisällyttämällä (suodattamalla vasemmalle, mikä kääntää nuolien suunnan). Sillä menemme sisään rajoituksin.R{\ displaystyle \ mathbb {R}}VS(U,R){\ displaystyle C (U, \ mathbb {R})}V⊂U{\ displaystyle V \ osajoukko U}VS(U,R){\ displaystyle C (U, \ mathbb {R})}VS(V,R){\ displaystyle C (V, \ mathbb {R})}

Huomautuksia ja viitteitä

1. (De) Lev Pontriaguine , "  Über den algebraischen Inhalt topologische Dualitätssätze  " , Mathematische Annalen , voi.  105,1931, s.  165-205 ( lue verkossa ).
2. Eduard Čech , "  Homologian yleinen teoria missä tahansa tilassa  ", Fundamenta Mathematicae , voi.  19,1932, s.  149-183 ( lue verkossa [PDF] ).
3. (in) Norman Steenrod , "  Universal homologiaryhmään  " , American Journal of Mathematics , vol.  58, n o  4,1936, s.  661-701 ( lue verkossa ), s. 664.
4. (in) Jean Dieudonne , A History of Algebrallinen ja Differential Topologia 1900-1960 , Birkhauser,1989( lue verkossa ).
5. (in) Samuel Eilenberg ja Saunders MacLane , "  General Theory of Equivalence  " , Transaction of the American Mathematical Society , voi.  58, n °  2 1945, s.  231-294 ( lue verkossa [PDF] ).
6. (in) Daniel Kan , "  varatoimittajat  " , Transaction of the American Mathematical Society , voi.  87, 1958, s.  294-329 ( lue verkossa [PDF] ).

Lähteet

• Régine ja Adrien Douady , Algebra ja Galois teoriat [ yksityiskohtainen painos ]
• N. Bourbaki , Algebra , luvut 1-3

<img src="https://fr.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1x1" alt="" title="" width="1" height="1" style="border: none; position: absolute;">