Radian

Tiedot
Radian
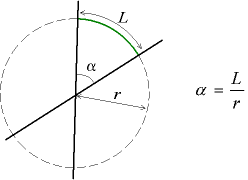Määritelmä kulma radiaaneina.
Järjestelmä	Kansainvälisestä järjestelmästä johdetut yksiköt
Yksikkö…	Tasokulma
Symboli	rad
Tulokset
1 rad sisään ...	on yhtä suuri kuin...
täysi käännös	2 π rad

Radiaani (symboli: rad ) on yksikkö, jotka on johdettu kansainvälisestä järjestelmän , joka mittaa tasossa kulmat . Vaikka sanan " radiaani " keksi 1870-luvulla Thomas Muir ja James Thomson , matemaatikot ovat pitkiä kulmamittauksia käyttäneet kehän ja säteen pituuden suhdetta yksikkönä.

Määritelmä

Tarkastellaan kulmasektoria, joka muodostuu kahdesta erillisestä samanaikaisesta linjasta , ja ympyrän , jonka säde r on piirretty tasolle, joka sisältää nämä kaksi viivaa, jonka keskipiste on viivojen leikkauspiste. Sitten arvo kulman radiaaneina on pituuden suhde L on kaaren ympyrän toimesta linjat ja säde r .

Kulman radiaaneina siepataan on kehälle tämän ympyrän kaaren, jonka pituus on yhtä suuri kuin säde. Täysi ympyrä edustaa 2 π radiaania, jota kutsutaan täyskulmaksi .

Käyttö radiaania on välttämätöntä, kun yksi on peräisin tai integroi trigonometrinen funktio tai vaikka ONE käyttää rajoitettua kehitystä tämän trigonometristen: todellakin, kulman pysty löytyy tekijä, ainoastaan arvo radiaaneina on yhteen suuntaan. Siksi trigonometristen funktioiden laskeminen Taylor-sarjalla olettaa kulmien ilmaisemisen radiaaneina, aivan kuten Eulerin kaavan soveltaminen , joka esitti sen määrittelemällä, että kulmat oli mitattava kaaren säteen pituudella että he sieppaavat yli vuosisadan ennen radian- termin keksimistä .

Pienet kulmat

Pienillä radiaaneina ilmaistuilla kulmilla sin x ≈ tan x ≈ x .

Jos kulma on alle 0,17 radiaania (ts. ~ 10 °), virhe on alle 1%;
Jos kulma on alle 0,05 radiaania (eli ~ 3 °), virhe on alle 0,1%.

Topografian alalla , jossa käsittelemme heikkoja kulmia, käytämme kulma mil , käytännöllinen yksikkö, joka määritellään kulmaksi, jonka 1 mm : n pituus katkaisee 1 m : n etäisyydellä . Sitä käytetään esimerkiksi etäisyyden määrittämiseen tunnetun korkeuden henkilöstöstä mittaamalla sen näennäinen koko . Olosuhteissa, joissa se palvelee, tämä yksikkö tunnistaa milliradiaaniksi .

Suhteet asteiden, astetta ja radiaaneja

Yksi täysi kierros on yhtä suuri kuin 2 π radiaania, 360 astetta, 400 astetta.

Siksi,

Yksi radiaani on noin 57,3 ° tai 57 ° 18 '(360 ° 2π);
yksi aste on noin 17,5 milliradiota.

Asteen ja radiaanin muunnoskaavat ovat:

\ theta _ {{deg}} = \ theta _ {{rad}} \ cdot {180 \ over \ pi}

\ theta _ {{rad}} = \ theta _ {{deg}} \ cdot {\ pi \ yli 180}

Arvosanojen ja radiaanien väliset muuntokaavat ovat:

\ theta _ {{gra}} = \ theta _ {{rad}} \ cdot {200 \ over \ pi}

\ theta _ {{rad}} = \ theta _ {{gra}} \ cdot {\ pi \ yli 200}

. Joitakin erityisiä kulmia radiaaneina, asteina, asteina ja käännöksinä:

kulman nimi	arvo radiaaneina	arvo luokissa	arvo asteina	arvo vuorollaan
nolla kulma	0 rad	0 gon	0 °	0 p
milliradan	0,001	0,063 661 977 gon	0 ° 3 '26' 16 'tai 0.0573 °	0,00015915494 tr
	π / 6 rad	33333 333 gon	30 °	0,08333 p (1/12 p)
	π / 4 rad	50 gon	45 °	0,125 p (1/8 p)
radiaani	1 rad	63,661,977 gon	57 ° 17 ′ 44 ″ 48 ‴	0,1591549430919 p (1 / π / 2 p)
	π / 3 rad	666666666 gon	60 °	0,1666 p (1/6 p)
oikea kulma	π / 2 rad	100 gon	90 °	0,25 tr
	2π / 3 rad	133333333 gon	120 °	0,333 tr
	3π / 4 rad	150 gon	135 °	0,375 rpm
tasainen kulma	π rad	200 gon	180 °	0,5 tr
	5π / 4 rad	250 gon	225 °	0,625 tr
	3π / 2 rad	300 gon	270 °	0,75 kierrosta / min
	7π / 4 rad	350 gon	315 °	0,875 kierrosta / min
täysi kulma	2π rad	400 gon	360 °	1 p

Katso myös

Bibliografia

Richard Taillet, Loïc Villain ja Pascal Febvre, fysiikan sanakirja , Bryssel, De Boeck ,2013, "Radian", s. 569

Aiheeseen liittyvät artikkelit

Huomautuksia ja viitteitä

(sisään) AR Crathorne , " The Word" Radian " " , American Mathematical Monthly , voi. 19, n os 10-11,Loka-marraskuu 1912, s. 166 ( DOI 10.2307 / 2971878 , JSTOR 2971878 ).
(in) Robert J. Whitaker, " josta saatavaa" radiaanin '? " , The Physics Teacher (in) , voi. 32, n ° 7,Kesäkuu 1998, s. 444–445 ( DOI 10.1119 / 1.2344073 ).
Taillet, Villain and Febvre 2013 , s. 39.