Convolution-tuote

On matematiikka , konvoluutio tuote on bilineaarinen operaattori ja kommutatiivinen tuote , jota merkitään yleensä ” $*$ ”, joka, jossa on kaksi toimintoja $f$ ja $g$ samassa ääretön verkkotunnuksen, merkit vastaavat toisen toiminnon ” $f$ $*$ $g$ ” on tällä alalla, joka on mikä tahansa jälkimmäisen piste on yhtä suuri kuin koko alueen integraali (tai summa, jos se on erillinen ) kahdesta tämän pisteen ympärillä olevasta toiminnosta, painotettuna toisella funktiolla alkuperän ympärillä - nämä kaksi toimintoa kulkevat vastakkaisiin suuntiin toisistaan (välttämätön kommutatiivisuuden takaamiseksi).

Konvoluutiotuote yleistää liukuvan keskiarvon ajatuksen ja on lineaarisen suodattimen käsitteen matemaattinen esitys . Se koskee yhtä hyvin ajallista dataa (esimerkiksi signaalinkäsittelyssä ) ja paikkatietoa ( kuvankäsittelyssä ). In tilastojen , hyvin samanlaisen kaavan käytetään määrittämään rajat korrelaatio .

Konvoluutiotuotteen määritelmä

Kahden reaalisen tai monimutkaisen funktion $f$ ja $g$ konvoluutiotulo on toinen funktio, joka yleensä merkitään " $f * g$ " ja jonka määrittelee:

{\ displaystyle (f \ ast g) (x) = \ int _ {- \ infty} ^ {+ \ infty} f (xt) g (t) \, \ mathrm {d} t = \ int _ {- \ infty} ^ {+ \ infty} f (t) g (xt) \, \ mathrm {d} t}

tai vielä, ja sekvenssit (korvaamalla Lebesguen mitta , jonka laskenta toimenpide ):

{\ displaystyle (f \ ast g) (n) = \ summa _ {m = - \ infty} ^ {\ infty} {f (nm) g (m)} = \ summa _ {m = - \ infty} ^ {\ infty} {f (m) g (nm)}}

Sarjoissa puhumme Cauchy-tuotteesta (mutta seuraavassa käytämme vain "jatkuvaa" versiota).

Voimme pitää tätä kaavaa liukuvan keskiarvon ideana .

Jotta tämä määritelmä olisi mielekäs, $f: n$ ja $g: n on$ täytettävä tietyt hypoteesit; Esimerkiksi jos nämä kaksi funktiota ovat integroitavissa Lebesgue-mielessä (ts. ne ovat mitattavissa ja niiden moduulin integraali on äärellinen), niiden konvoluutiotulo on määritelty melkein kaikille x: lle ja se on itse integroitava. Yleisemmin, jos $f \in L p$ ja $g \in L q$ ja kanssa , niin $f$ $*$ $g$ $\in L$ $r$ : vrt. " Youngin eriarvoisuus kääntymisessä ". ${\ displaystyle {\ frac {1} {p}} + {\ frac {1} {q}} = 1 + {\ frac {1} {r}}}$ ${\ displaystyle p, q, r \ in [1, + \ infty]}$

Konvoluutiotuotteen ominaisuudet

Algebralliset ominaisuudet

Konvoluutiotuote on bilineaarinen , assosiatiivinen ja kommutatiivinen :

{\ displaystyle f \ ast (g + \ lambda h) = (f \ ast g) + \ lambda (f \ ast h)}

(mihin tahansa skalaariin

λ

);

{\ displaystyle (f \ ast g) \ ast h = f \ ast (g \ ast h)}

;

{\ displaystyle f \ ast g = g \ ast f}

. Esittely

Konvoluutiotuote on jakautuva lisäykselle:

${\ displaystyle {\ begin {aligned} (f \ ast (g + h)) (x) & {\ stackel {\ mathrm {def.}} {=}} \ int _ {- \ infty} ^ {+ \ infty} f (xt) (g (t) + h (t)) \, \ mathrm {d} t \\ & = \ int _ {- \ infty} ^ {+ \ infty} [f (xt) g ( t) + f (xt) h (t)] \, \ mathrm {d} t \\ & = \ int _ {- \ infty} ^ {+ \ infty} f (xt) g (t) \, \ mathrm {d} t + \ int _ {- \ infty} ^ {+ \ infty} f (xt) h (t) \, \ mathrm {d} t \\ & {\ stackrel {\ mathrm {def.}} { =}} (f \ ast g) (x) + (f \ ast h) (x). \ end {tasattu}}}$

Konvoluutiotuote on assosiatiivinen, kun otetaan huomioon integroitavat toiminnot (joihin Fubinin lause pätee ): ${\ displaystyle {\ begin {tasattu} ((f \ ast g) \ ast h) (y) & {\ stackel {\ mathrm {def.}} {=}} \ int _ {- \ infty} ^ {+ \ infty} \ left (\ int _ {- \ infty} ^ {+ \ infty} f ((yx) -t) g (t) \, \ mathrm {d} t \ oikea) h (x) \, \ mathrm {d} x \\ & = \ int _ {- \ infty} ^ {+ \ infty} \ int _ {- \ infty} ^ {+ \ infty} f (yT) g (Tx) h (x) \ , \ mathrm {d} x \, \ mathrm {d} T \\ & = \ int _ {- \ infty} ^ {+ \ infty} f (yT) \ vasemmalle (\ int _ {- \ infty} ^ { + \ infty} g (Tx) h (x) \, \ mathrm {d} x \ right) \, \ mathrm {d} T \\ & {\ stackrel {\ mathrm {def.}} {=}} ( f \ ast (g \ ast h)) (y) \ end {tasattu}}}$ missä joko ja . $T = x + t$ $t = Tx$ ${\ displaystyle \ mathrm {d} t = \ mathrm {d} T}$
Konvoluutiotuote on kommutatiivinen. Se näkyy helposti toimimalla seuraava muuttujan muutos : ${\ displaystyle {\ begin {tasattu} (f \ ast g) (x) & {\ stackrel {\ mathrm {def.}} {=}} int {{\ \ infty} ^ {+ \ infty} f xt) g (t) \, \ mathrm {d} t \\ & = \ int _ {+ \ infty} ^ {- \ infty} f (T) g (xT) \, \ mathrm {d} (-T ) \\ & = \ int _ {- \ infty} ^ {+ \ infty} f (T) g (xT) \, \ mathrm {d} T \; \\ & {\ stackrel {\ mathrm {def.} } {=}} (g \ ast f) (x) \ end {tasattu}}}$ missä $T = x - t$ , olkoon $t = x - T$ ja $d t = d (- T )$ .

Pseudorengas

Lisäyksen ja konvoluutiotuotteen mukana toimitettava integroitavien toimintojen joukko muodostaa siten pseudorenkaan , toisin sanoen ei-yhtenäisen renkaan . Jos tämä rengas olisi yhtenäinen, yksikköelementin $δ$ tulisi tarkistaa (mahdollisten $x: n$ ja minkä tahansa funktion $f suhteen$ ):

{\ displaystyle f (x) = \ int _ {- \ infty} ^ {+ \ infty} f (t) \ delta (xt) \, \ mathrm {d} t}

Voidaan helposti tarkistaa, että tämä on mahdollista vain, jos $δ$ on Dirac-jakauma … joka ei ole funktio.

Konvoluutiotuotteen hyvän yleistämisen luonnollinen kehys on jakautumisteoria , mutta sitä ei käsitellä tässä artikkelissa. Löydämme jakeluille omistetusta artikkelista tarkan määritelmän konvoluutiotuotteesta tässä tapauksessa sekä tutkimuksen sen pääominaisuuksista.

Yhteensopivuus käännösten kanssa

Konvoluutiotuote on yhteensopiva ajallisten käännösten kanssa. Jos merkitsemme $τ h: lla$ käännöksen funktioiden avulla

{\ displaystyle (\ tau _ {h} f) (x) = f (xh)}

niin

{\ displaystyle (\ tau _ {h} f) \ ast g = \ tau _ {h} (f \ ast g).}

Suurissa puitteissa konvoluution toimenpiteitä ,

{\ displaystyle \ tau _ {h} f = \ delta _ {h} \ ast f}

missä $δ h$ merkitsee Dirac-massaa h , ja yhteensopivuus käännösten kanssa on vain välitön seuraus toimenpiteiden konvoluutiotuotteen assosiatiivisuudesta:

{\ displaystyle (\ tau _ {h} f) \ ast g = (\ delta _ {h} \ ast f) \ ast g = \ delta _ {h} \ ast (f \ ast g) = \ tau _ { h} (f \ ast g).}

Tätä ominaisuutta on myös verrattava konvoluutiotuotteiden sovelluksiin suodattamiseen .

Pariteetti

Konvoluutio seuraa merkki sääntöä varten yhdenvertaisuus toiminnot :

f * g

on parillinen (vastaavasti pariton), jos

f: llä

g: llä

on sama pariteetti (tai vastakkaiset pariteetit). Esittely

Merkitään $I$ involuution määritelty ja tarkista, että . ${\ displaystyle (Jos) (x) = f (-x)}$ ${\ displaystyle I (f \ ast g) = (Jos) \ ast (Ig)}$

{\ displaystyle {\ begin {tasattu} (I (f \ ast g)) (x) & = (f \ ast g) (- x) \\ & = \ int _ {- \ infty} ^ {+ \ infty } f (-xt) g (t) \, \ mathrm {d} t \\ & = \ int _ {- \ infty} ^ {+ \ infty} f (-x + u) g (-u) \, \ mathrm {d} u \\ & = \ int _ {- \ infty} ^ {+ \ infty} (Jos) (xu) (Ig) (u) \, \ mathrm {d} u \\ & = (( Jos) \ ast Ig) (x). \ Loppu {tasattu}}}

Tämä ominaisuus yhdistettynä muunnettavaan muuttamattomuuteen tekee mahdolliseksi todistaa, että tasaisen funktion aiheuttama konvoluutiotulo säilyttää toimintojen aksiaaliset symmetriat:

Jos

g

on parillinen ja jos

f ( x - h ) = f (- x - h ),

niin

( f * g ) ( x - h ) = ( f * g ) (- x - h )

. Esittely

Ensimmäinen yhtälö vastaa yhtälöä . Voimme päätellä ${\ displaystyle \ tau _ {h} (f) (x) = \ tau _ {h} (f) (- x)}$

{\ displaystyle ((\ tau _ {h} f) \ ast g) (x) = ((\ tau _ {h} f) \ ast g) (- x) = \ tau _ {h} (f \ ast g) (x) = \ tau _ {h} (f \ ast g) (- x)}

mikä on ilmoitettu tulos.

Konvoluutiotuotteen integrointi

Meillä on (soveltamalla Fubinin teoreemaa ) kaava: ${\ displaystyle \ int _ {- \ infty} ^ {+ \ infty} (f \ ast g) (t) \, \ mathrm {d} t = \ left (\ int _ {- \ infty} ^ {+ \ infty} f (t) \, \ mathrm {d} t \ oikea) \ vasen (\ int _ {- \ infty} ^ {+ \ infty} g (t) \, \ mathrm {d} t \ right). }$

Johtaminen

Tapauksessa yhden muuttujan, jos $f$ (esimerkiksi) on luokan $C 1$ ja jos $f$ , $f '$ ja $g$ kuuluvat $L 1$ sitten

{\ displaystyle (f * g) '= f' * g}

Yleisemmin tapauksessa tehtäviä useita muuttujia olemme

{\ displaystyle {\ frac {\ partitali} {\ osittainen x_ {i}}} (f * g) = {\ frac {\ osittainen f} {\ osallinen x_ {i}}} * g}

Konvoluutiotuote ja Fourier-muunnos

Fourier-muunnos konvoluution tuote saadaan kertomalla Fourier-muunnoksessa toiminnot:

jos $f$ ja $g$ ovat integroitavia, niin ${\ displaystyle {\ mathcal {F}} (f \ ast g) = {\ mathcal {F}} (f) {\ mathcal {F}} (g) ~;}$
jos $f$ on integroitava ja jos $g$ on neliöintegroitava , meillä on myös

${\ displaystyle {\ mathcal {F}} (f \ ast g) = {\ mathcal {F}} (f) {\ mathcal {F}} (g) {\ text {siis}} f \ ast g = { \ mathcal {F}} ^ {- 1} \ vasen ({\ mathcal {F}} (f) {\ mathcal {F}} (g) \ oikea) ~;}$

jos $f$ ja $g$ ovat neliön integroitavia, niin ${\ displaystyle f \ ast g = {\ mathcal {F}} ^ {- 1} \ vasen ({\ mathcal {F}} (f) {\ mathcal {F}} (g) \ oikea)}$

missä merkitsee Fourier-muunnosta ja käänteistä Fourier-muunnosta ("konvoluutiolause"). ${\ mathcal {F}}$ ${\ displaystyle {\ mathcal {F}} ^ {- 1}}$

Nämä kaavat on rajoitettu Schwartz-avaruuteen , sitten ne ulottuvat osittain Fourier-muunnokseen lauhkeille jakaumille , joita käytetään esimerkiksi kompaktilla tuella jakelun karkaistun jakauman konvoluutioon . Yleisemmin, jos S ja T ovat kaksi karkaistua jakaumaa , joista toinen on konvolveri , niin niiden Fourier-muunnokset ovat karkaistuja jakaumia, joista toinen on kertoja , ja ne todentavat: ${\ displaystyle {\ mathcal {F}} (S \ ast T) = {\ mathcal {F}} (S) {\ mathcal {F}} (T) {\ text {siis}} S \ ast T = { \ mathcal {F}} ^ {- 1} \ vasen ({\ mathcal {F}} (S) {\ mathcal {F}} (T) \ oikea).}$

Tässä yhteydessä Dirac-jakauma ( neutraali konvolveri ) ja vakiofunktio $1$ (neutraali kerroin) ovat kaksi karkaistua jakaumaa (jopa) Fourier-muunnokset toisistaan.

Fourier-muunnosten konvoluutiotuotteen laskennan pääkohde on, että nämä operaatiot ovat tietokoneelle ajoissa halvempia kuin integraalin suora laskenta.

Konvoluutiotuotteen käyttö

Konvoluutiotuotetta käytetään signaalinkäsittelyssä käytettäessä suodattimia ( alipäästö , ylipäästö , kaistanpääsy ). Jos meillä on saapuva signaali $e ( t )$ ja suodatinelementti, jolla on siirtofunktio $h ( t ),$ lähtösignaali $s ( t )$ on näiden kahden toiminnon konvoluutio: ${\ displaystyle s = e \ ast h}$ (konvoluutiotuote) ja $S ( f ) = E ( f ) H ( f )$ (kahden funktion yksinkertainen tulo)jossa $E ( f )$ , $S ( f )$ ja $H ( f )$ on Fourier-muunnokset aikafunktiot $e ( t )$ , $s ( t )$ ja $h ( t )$ .
In kristallografia , konvoluutio lause käytetään suoraan menetelmiä määrittää vaiheessa on rakenne tekijöitä , kun määritetään kiderakenne .
Todennäköisyys, todennäköisyys tiheys summa kahden riippumattoman todellinen satunnaismuuttujaa (tiheys) on konvoluutio tuote todennäköisyys tiheydet näiden kahden riippumattoman muuttujan, kuten nähdään käyttäen muuttujanvaihdoilla .
Konvoluutiotuotteiden toinen käyttö on kvanttimekaniikkaa, jossa konvoluutiotuotteita tuotetaan rintaliivit ja ket- aaltofunktiot .
Yleensä voimme kirjoittaa monia fyysisiä ongelmia vastaavat lineaariset differentiaaliyhtälöt operaattorin konvoluutiotuloksena järjestelmää kuvaavalla toiminnolla. Voimme sitten ratkaista ongelman yleisellä tavalla määrittämällä operaattorin käänteisversio (kutsutaan Greenin funktioksi ). Joseph Fourier oli tämän menetelmän lähtökohdassa, kun hän yritti ratkaista lämpöyhtälön . Nykyaikaisen muotoilu on täytynyt odottaa saapumista teorian jakelut käyttöön Laurent Schwartz .
Konvoluutiotuote yleistää ryhmän monet algebrat, esimerkiksi äärellisen ryhmän algebrat . Jos ryhmä on lisäksi abelin, niin äärellisen abelian ryhmän harmonisen analyysin teoria mahdollistaa kaikkien konvoluutiotuotteen klassisten tulosten määrittämisen.
Vuonna syvällisen oppimisen , konvoluutio operaattorit ovat pankit suodattimia on neuroverkkojen Convolutive varten konenäön tai luonnollisen kielen käsittely .

Mittojen konvoluutiotuote

Toimenpiteiden muuttaminen todelliselle linjalle

Laajemmassa voimme määritellä konvoluutio tuotetta kahden toimenpiteitä koskevat seuraavien todennäköisyyspohjaiset tulkinta: kun todennäköisyys lakeja $u$ ja $ν$ kahden riippumattoman todellista satunnaismuuttujaa ei molemmat ovat tiheydet suhteessa mitta Lebesgue , laki niiden summa on konvoluutio on $μ$ mukaan $ν$ , merkitty $μ$ $*$ $ν$ ja määritellään jonakin Borel of mukaan ${\ displaystyle (\ mathbb {R}, {\ mathcal {B}} (\ mathbb {R})),}$ $\ mathbb {R},$

\ mu \ ast \ nu (A) = \ int _ {{\ mathbb {R} ^ {2}}} \ 1_ {A} (x + y) \, \ mu ({\ mathrm d} x) \, \ nu ({\ mathrm d} y).

Integraali funktio θ suhteen toimenpiteen $μ * ν$ saadaan

\ int _ {{\ mathbb {R}}} \ \ theta (s) \, (\ mu \ ast \ nu) ({\ mathrm d} s) \ = \ \ int _ {{\ mathbb {R} ^ {2}}} \ \ theta (x + y) \, \ mu ({\ mathrm d} x) \, \ nu ({\ mathrm d} y).

Konvoluutio tuote $u * v$ on kuva toimenpide funktion φ , määritellään mukaan $φ$ $($ $x$ $,$ $y$ $) =$ $x$ $+$ $y$ , ja tuote toimenpiteen $u$ $\otimes$ $v$ . Erityisesti, jos molemmilla $μ$ ja $ν$ on tiheydet, vastaavasti $f$ ja $g$ , suhteessa Lebesgue-mittaukseen, niin $μ$ $*$ $ν:$ lla on myös tiheys Lebesgue-mittaukseen nähden, ja yksi sen tiheyksistä on $f$ $*$ $g$ . $\ mathbb {R} ^ {2}$

Toimenpiteiden muuttaminen kommutatiiviselle ryhmälle

Tämä konvoluutiotuotteen määritelmä voidaan laajentaa välittömästi kommutatiiviseen topologiseen ryhmään $( G , \oplus),$ jolla on borelian heimo , välittömästi: minkä tahansa $G$ : n borelilaisen $A$ osan osalta

{\ displaystyle \ mu \ ast \ nu (A) = \ int _ {G ^ {2}} \ 1_ {A} (x \ oplus y) \, \ mu (\ mathrm {d} x) \, \ nu (\ mathrm {d} y).}

Integraali funktio θ suhteen toimenpiteen $μ * ν$ saadaan

{\ displaystyle \ int _ {G} \ \ theta (s) \, (\ mu \ ast \ nu) (\ mathrm {d} s) \ = \ \ int _ {G ^ {2}} \ \ theta ( x \ oplus y) \, \ mu (\ mathrm {d} x) \, \ nu (\ mathrm {d} y).}

Käsite Haar mitta ryhmä $G$ on sitten kirjoitettu suhteen konvoluution tuote: $μ$ on Haar mitta $G$ , jos ja vain jos, mille tahansa elementti $g$ ja $G$ ,

{\ displaystyle \ delta _ {g} \ ast \ mu = \ mu.}

Jos ryhmä ei ole kommutatiivinen, voimme silti määritellä konvoluutiotuotteen määrittämällä konvoluutio vasemmalle tai oikealle.

Yleisemmin voimme määritellä konvoluutiotuotteen ryhmän toiminnalle . Olkoon $G$ mitattava ryhmä, joka vaikuttaa mitattavaan tilaan K , havaitun toiminnan. ja ovat $μ$ räätälöityjä $G$ ja $ν$ räätälöity K . Määritämme konvoluutiotuotteen kaavalla

{\ displaystyle \ mu * \ nu (A) = \ int _ {K} \ int _ {G} {\ mathsf {1}} _ {A} (gx) \, \ mu (\ mathrm {d} g) \, \ nu (\ mathrm {d} x)}

missä A on mitattava osa K: sta .

Se on K: n mitta . Jos K = G ja jos toiminto on kertolasku (tai vasen tai oikea kertolasku, jos ryhmä ei ole kommutatiivinen), löydämme konvoluution tuloksen edellä kuvatuista ryhmistä.

Popularisoitu lähestymistapa

Yksinkertaisin tapa edustaa konvoluutiotuotetta on tarkastella Dirac-funktiota δ $8 a ( x )$ ; tämän “funktion” arvo on 0, jos x ≠ a ja sen integraali on arvoltaan 1. Tämä saattaa tuntua intuitiiviselta, mutta voimme kuvitella sen rajaksi funktioiden, kellokäyrien tai suorakulmioiden sarjan, joilla kaikilla on sama pinta 1, mutta yhä ohuempi (siksi korkeampi ja korkeampi); kun käyrien leveys on kohti 0, sen korkeus on kohti + ∞, mutta pinta-ala on yhtä suuri kuin 1. Käytännöllisistä syistä esittelemme diracia tikkuna, joka on sijoitettu a : n korkeuteen ja korkeuteen 1.

Dirac $5: n muodostaman$ konvoluution tulo vastaa alkutoiminnon käännöstä arvolla a

f \ ast \ delta _ {a} (x) = f (xa)

Tulos funktion konvoluutiosta diracilla

Näemme, että δ 0 jättää funktion invariantiksi, se on konvoluutiotuotteen neutraali elementti

f \ ast \ delta _ {0} (x) = f (x-0)

Jos tarkastelemme nyt konvoluutiotuotetta kahden diracin ( $α δ$ $a$ $+ β δ$ $b$ ) painotetulla summalla , saadaan kahden käännetyn käyrän päällekkäisyys.

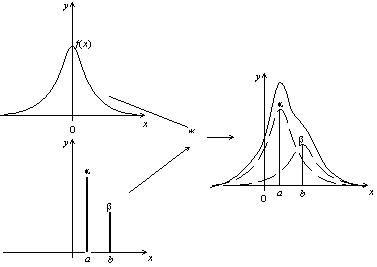
Funktion konvoluutiotulo kahden diracin painotetulla summalla

Tarkastellaan nyt porttitoimintoa Pa , b ; se on funktio, jonka arvo on 1 / ( ba ) a: n ja b : n välillä ja 0 muualla (sen integraali on 1: n arvoinen). Tämä toiminto voidaan nähdä diracien peräkkäisenä. Konvoluutio $f$ mukaan P a, b näin ollen saadaan vetämällä $f$ aikavälinä [ ; b ]. Saamme $f:$ n "suurennuksen" .

Funktion konversiotuote porttitoiminnolla

Jos tarkastelemme nyt mitä tahansa funktiota $g$ , voimme nähdä $g$ diracien peräkkäisenä painotettuna $g: n$ arvolla tarkasteltavassa pisteessä. $F$ : n konvoluutiotulo $g: llä$ saadaan siis vetämällä funktiota $f$ ja laajentamalla sitä $g:$ n arvon mukaan .

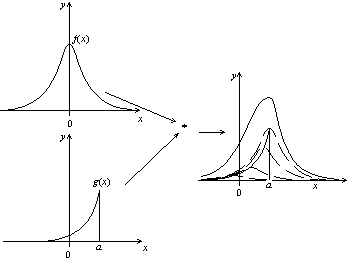
Funktion konvoluutiotulo millä tahansa funktiolla

Konvoluution ja suodatuksen tuote

Konvoluutiotuote liittyy suodatuksen käsitteeseen kahdessa olosuhteessa, nimittäin suodattimen lineaarisuudessa ja riippumattomuudessa ajan suhteen ( invariantti järjestelmä ). Näistä kahdesta ehdosta voidaan muodostaa konvoluutiooperaattori. Konvoluutio vastaa suodattimen vastausta annettuun tuloon (huomattu $e ( t )$ ). Suodattimelle on täysin tunnusomaista sen impulssivaste $h ( t )$ . Laitetaan yhtälöön, suodattimen vaste on $s ( t ) = { h * e } ( t )$ .

Konvoluutiooperaattorin rakenne suunnitellaan seuraavasti. Ensinnäkin olemme kiinnostuneita suodattimelle asetetuista kahdesta ehdosta. Merkitään $f ( e )$ suodattimen suorittamalla suodatuksella tuloon e . Suodattimen lineaarisuus tarkoittaa, että:

f (\ lambda e) = \ lambda f (e)

f (e_ {1} + e_ {2}) = f (e_ {1}) + f (e_ {2})

Voidaan todeta, että suodattimen vaste nollasignaalille on nolla. Ajan riippumattomuus tiivistetään seuraavasti:

f (e ^ {d}) = (f (e)) ^ {d}

missä $e d$ on signaalin $e$ viivästyttämä määrä $d$ .

Sieltä voimme rakentaa lineaarisen ja ajasta riippumattoman suodattimen vasteen tuloon $e ( t )$ . Todellakin, kuten suodatin on lineaarinen, voimme hajota signaali $e ( t )$ itsenäisiä osia, käyttäen joukkoa signaaleja $e i$ , jossa kompakti erilliset tuet niin, että . Signaalin kukin osa injektoidaan suodattimeen ja sitten eri vastaukset summataan. Näin ollen suodatus: . Tämä ajallinen hajoaminen $e$ $($ $t$ $)$ voidaan suorittaa rekursiivisesti signaalien $e$ $i$ $($ $τ$ $)$ . Lopulta saamme sarjan signaaleja, joiden tuki laskee pisteeseen. Nämä signaalit, jotka ovat alkeellisia, koska niitä ei voida hajottaa ajan myötä, vastaavat kukin Dirac-jakaumaa $δ$ $($ $t$ $-$ $τ$ $), joka on$ keskitetty $τ$ : een amplitudilla $e$ $($ $τ$ $)$ , impulssi kirjoitetaan $δ$ $($ $t$ $-$ $τ$ $)$ $e$ $($ $τ$ $)$ . Riittää, kun lisäät kaikki pulssit muuttujaa $τ$ pitkin signaalin $e$ $($ $t$ $)$ saamiseksi : $e (t) = \ Sigma _ {i} e_ {i} (t)$ $f (e) = \ Sigma _ {i} f (e_ {i})$

{\ displaystyle e (t) = \ int \ delta (t- \ tau) e (\ tau) \, \ mathrm {d} \ tau}

Suodatusoperaatiota sovelletaan $e ( t ): een$ . Koska suodatin on lineaarinen ja ajasta riippumaton, meillä on:

{\ displaystyle {\ begin {tasattu} f (e) & = \ int f (\ delta (t- \ tau) e (\ tau)) \, \ mathrm {d} \ tau \\ & = \ int e ( \ tau) f (\ delta (t- \ tau)) \, \ mathrm {d} \ tau & {\ text {(lineaarisuus)}} \\ & = \ int e (\ tau) (f \ circ \ delta ) (t- \ tau) \, \ mathrm {d} \ tau & {\ text {(aikariippumattomuus).}} \ end {tasattu}}}

Suodattimen $f$ vastetta impulssiin $δ ( t )$ kutsutaan suodattimen $h ( t )$ impulssivasteeksi . Lopuksi meillä on:

{\ displaystyle f (e) = \ int e (\ tau) h (t- \ tau) \, \ mathrm {d} \ tau}

joka ei ole mikään muu kuin konvoluutio.

Lopuksi: jos suodatin on lineaarinen ja ajasta riippumaton, niin sille on täysin tunnusomaista sen vaste $h ( t )$ ja suodattimen vaste tulossa $e ( t )$ on konvoluutiooperaattorin antama.

Toinen lineaaristen ja ajasta riippumattomien suodattimien perustavanlaatuinen johtopäätös: jos syötämme signaalin $e ( t ) = e 2 π j ft$ , lähtösignaali on:

{\ displaystyle {\ begin {aligned} s (t) & = \ int \ mathrm {e} ^ {2 \ pi \ jmath f \ tau} h (t- \ tau) \, \ mathrm {d} \ tau \ \ & = \ int \ mathrm {e} ^ {2 \ pi \ jmath f (t- \ tau)} h (\ tau) \, \ mathrm {d} \ tau \\ & = \ mathrm {e} ^ { 2 \ pi \ jmath ft} \ int \ mathrm {e} ^ {- 2 \ pi \ jmath f \ tau} h (\ tau) \, \ mathrm {d} \ tau \\ & = \ mathrm {e} ^ {2 \ pi \ jmath ft} H (f). \ Loppu {tasattu}}}

Signaali $s ( t )$ on myös muodoltaan $e 2 π j ft$ oleva signaali tekijään $H ( f ) asti$ . Tämä tekijä ei ole mikään muu kuin Fourier-muunnos on $h ( t )$ .

Huomautuksia ja viitteitä

Katso myös

Aiheeseen liittyvät artikkelit

Bibliografia

Marc Briane ja Gilles Pagès, integraatioteoria: konvoluutio ja Fourier-muunnos , Pariisi, Vuibert ,2012, 365 Sivumäärä ( ISBN 978-2-311-00738-1 )

Ulkoiset linkit

( fr ) Animaatio Johns Hopkinsin yliopistosta, joka selittää kääntymisen graafisesti
Viva la Convolution : kääntymisen soveltaminen akustiikkaan